Blog

At my job, it's not too often I have a use for "exotic" data structures. Most of the time, a simple HashMap, Set, or List (vector) will do the job. However recently we had a situation come up where we got to apply a Bloom Filter to solve our problem. If your unfamiliar with Bloom Filters, they are a space optimized, probabilistic set data structure. They have a neat property where they can tell you that something is probably in a set, or definitely not in a set. So basically, they are a great if you don't care about false positives, but must always have true negatives. They are also a good choice if you have limited space, or want to know exactly how much space your using because they don't grow or shrink no matter how much data you "store" in them. However, the downside is that the more data you store, more more likely a false positive will occur. In our case, we could not store the full data set in memory, so a Bloom Filter was a perfect fit.

Bloom filters are a very simple data structure. They are simple an array of bits (bitmap). These bits get set as you add data to the filter. When you add new data to the filter, the data is run through a hash function, and that hash function is used to select the index of the bit to flip to true. Normally you use a few hashes, or different parts of the same hash to set a few bits per piece of data. Ideally, your hash produces values in a nice uniform distribution. Lets take a look at an example.

In this example, I use the Murmur2 hash 4 times with 4 different seed values. The output of the Murmur2 hash is a 32 bit unsigned number. I can then take this number and use the modulus to get an index. Now if I wanted to check if an item was in the set, I would just do the exact same hashing and get the same indexes, and then verify that those indexes are all 1's. If there are any 0's then this item was definitely never added to the set.

Now, it should be clear why this data structure has false positives. It's because you only have a limited set of hashes to map values into, so there can be collisions. Lets say for example that I have added "Hello" into the filter, and it happens to map to bits 1, 2, 3 and 4. Later I check if the word "Boston" is in the set, and it also happens to map to bits 1, 2, 3 and 4. Now I have a false positive. However, the larger we make the bit map, and the more uniform the output of the hash function is, the less likely we get a collision. It should also be clear why you don't get false negatives. If any of the indexes are false, or 0, then the whole thing is false.

Now that we understand how a Bloom Filter works, let's go ahead and implement one of our own. For this project I will be using C++. I will make all of the code available on my GitHub.

  class IBloomFilter {
    public :
    virtual void add(const std::string& s) = 0;
    virtual bool contains(const std::string& s) const = 0;
    virtual void clear() = 0;
    virtual double getProbabilityOfFalsePositive() const = 0;
    virtual unsigned int getCount() const = 0;
    virtual unsigned long int getBitCount() const = 0;

    protected :
    virtual ~IBloomFilter(){};
  };

Here is the interface that I created that defines what a Bloom Filter can do at a high level. Notice that there is no remove() function. This is because the same thing that can cause a false positive, can also cause multiple removals. Using the above example, if I tried to remove "Boston" I would also remove "Hello" and every other word that even partially maps to that sequence of bits.

I decided to code up the Bloom Filter in two different ways. A fixed size Bloom Filter where you specify the number of bits you want in the bitmap, and a dynamic Bloom Filter where you specify the number of elements you want to store, along with a worst case probability of false positives. Given this data it will generate a bit array of the proper size. First, lets take a look at the header for the FixedBloomFilter.

template <std::size_t N>
class FixedBloomFilter : public IBloomFilter {
  std::unique_ptr<std::bitset<N>> bitmap;
  unsigned long int m;
  unsigned int c;
  unsigned int k;
  std::vector<uint32_t> seeds;

  public :
  FixedBloomFilter();
  void add(const std::string& s);
  bool contains(const std::string& s) const;
  void clear();
  double getProbabilityOfFalsePositive() const;
  unsigned int getCount() const;
  unsigned long int getBitCount() const;
};

For the fixed size filter, I decided to use the std::bitset, as it is the ideal structure to store bits in. Next I define a few needed values. m is the number of bits, c is the current count of elements stored in the filter, k is the number of hashes I run on each entry, and seeds will hold the seeds for those hashes so each hash produces a different result. For the FixedBloomFilter we know these values, so we don't need to calculate them, but in the DynamicBloomFilter we will calculate these on the fly.

For both Bloom Filters, we will still calculate the error probability the same way using the following equation.

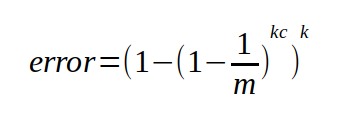
This will give us the worst case probably of getting a false positive. I say worst case because I found that in practice the real chance of false positives to be lower, sometimes by half or more. I suspect because there are certain "non-sane" value that will never be checked. For example, if my Bloom Filter is holding English words, and I want to compare the words in two books, chances are I will never check for gibberish words like "hvieioe", however this equation still accounts for that.

Now, for the DynamicBloomFilter I take into the constructor the maximum number of elements I expect the filter to hold, and the desired worst case probability that I want. Using those values, I can calculate the exact number of bits, and the number of hashes that I will need to fulfill these requirements.

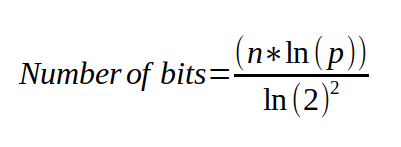
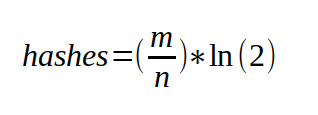
class DynamicBloomFilter : public IBloomFilter {
  unsigned long m;
  unsigned int n;
  double p;
  unsigned int c;
  std::vector<bool> bitmap;
  std::vector<uint32_t> seeds;

  public : 
  explicit DynamicBloomFilter(unsigned int n, double desired_p);
  void add(const std::string& s);
  bool contains(const std::string& s) const;
  void clear();
  double getProbabilityOfFalsePositive() const;
  unsigned int getCount() const;
  unsigned long int getBitCount() const;
};

To see the details of the implementation, check out my source code repo on github. For brevity, I'm just going to show the add and contains code here so you can see the implementation.

void DynamicBloomFilter::add(const std::string& s) {
  const void* ptr = reinterpret_cast<const void*>(s.data()); 

  std::for_each(seeds.begin(), seeds.end(), [=, this](const uint32_t& seed) {
      uint32_t h = MurmurHash2(ptr, s.size(), seed);
      bitmap[h%m] = true;
  });

  c++;
}

bool DynamicBloomFilter::contains(const std::string& s) const {
  const void* ptr = reinterpret_cast<const void*>(s.data()); 

  return std::all_of(seeds.begin(), seeds.end(), [=, this](const uint32_t& seed) {
      uint32_t h = MurmurHash2(ptr, s.size(), seed);
      return bitmap[h%m];
  });
}

This code should look just like the picture that I showed above. For both adding and checking we hash the input value using the MurmurHash2() function. The only difference is that when adding, we set those bits to true (or 1), and when checking we just check that they are all true (or 1's).

Now that we have our two versions of the Bloom Filter, how do they perform? First lets take a look at the dynamic filter. This filter takes in two parameters, the expected number of elements to be stored in the filter, and the desired probability to a false positive. For my example, I am using the /usr/share/dict/cracklib-small, which is a small dictionary file containing 52,875 english words. My verification set is /usr/share/dict/american-english, which is a larger dictionary containing 102,305 words. When I create my new DynamicBloomFilter I set the max expected values to be 52875 and the desired error probability to be 0.01. Here are the results.

BloomFilter is 61.8663 K bytes
Bloom Filter loaded with 52876 words
Error probability: 0.0101441
Bloom Filter matched verification set 99.3783%
Actual Error Probability: 0.00621664

As you can see, the DynamicBloomFilter was able to take in our parameters and create the optimal filter size, and hash count to achieve our desired probability. It was able to do it in just under 62K of memory. Keep in mind that my actual data set was 468K. So that is a 7.5X reduction in size, with 99.4% accuracy. Not too bad.

For the FixedBloomFilter we can get similar results as long as we use the correct size for the bitmap. Using the smallest size FixedSize::TINY, we only get an 8KB filter, and a terrible 76.98% accuracy on our test set. However once we jump up one level to the FixedSize::SMALL, now we have a 128KB filter, with 99.9% accuracy. However, compared to the Dynamic filter, we are double the size and don't gain much accuracy. Something to consider when choosing your implementation.

BloomFilter is 128 K bytes
Bloom Filter loaded with 52876 words
Error probability: 0.00111332
Bloom Filter matched verification set 99.9365%
Actual Error Probability: 0.000635349

The DynamicBloomFilter is better when you know the size of the set your going to load into it, and just want to control for the error probability. The FixedBloomFilter is great when you have space constraints, or you don't know how much data your going to load, but just want to have a probabilistic way to knowing if you have "seen this before" (like for caching schemes). Both have their pros and cons, so I leave it to you to decide which way works better for your application. Ultimately in our application, we just chose a very large filter, we didn't know the upper limit of items we were going to add, and because even a few hundred megabytes was still gigabytes smaller then our actual data set.